◎莫丽美
(杭州市临平区乔司中学,浙江 杭州 311199)
近年来,中考数学试卷中的几何题目多为书本、作业本中习题的变式.几何证明不仅是初中阶段几何学习的核心内容,也是培养学生几何逻辑思维能力的重要推手.在以往的教学过程中,笔者发现学生中总有一些看似学习很认真,但几何证明就是学不好的学生.为此,笔者对学生进行了几何证明学习困惑的问卷调查,结果显示:学生的困惑主要集中在“推理过程的书写怎么样才算合理?证明思路的寻找怎么样才能快捷有效?辅助线的添加怎么样才能恰到好处?”三个方面.针对上述困惑,笔者提出了“品·寻·悟”的破解思路,进而实现“以简驭繁,化繁为简”.本文对其具体实施加以阐述,旨在交流与共勉.
所谓的“品”,主要是“夯实基础—认识基本图形—引导体验”这一过程.知识的建立离不开活动载体与基本的活动经验,现行的平面几何基本图形分为两级:第一级为点、线、三角形、四边形、圆等图形;
第二级为课本中的概念、基本事实、定理、推论所对应的图形.初中几何证明题中的基本图形多为第二级基本图形,且当题目较为复杂时则需添加辅助线用以构造基本图形.
(一)利用好每节几何新授课
教师在每节新授课都应同时展示文字语言、符号语言和图形语言,让学生感受文字语言、符号语言和图形语言的转译过程.例如,浙教版八上第一章第五节三角形全等判定中的三个基本事实和一个推论的三种表述形式的展现.每一个性质的得出都让学生去尝试推导,即使有论据不充分的情况,但及时指正后也会收获较好的效果.例如,浙教版八上第一章的“线段垂直平分线的性质”的讲解,可以先给出垂直平分线的定义(当然要配合几何语言),再探究其性质,探究后再用已有知识去验证其性质.课堂是学生学习的重要场地,课堂学习是学生能力提升的重要途径,教师要用好这个场地,使学生的能力在课堂情境中得以提升.例如浙教版八上第二章第三节等腰三角形的性质定理(2)中“等腰三角形三线合一”的证明过程,教师可以引导学生从等腰三角形的顶角平分线,既是底边上的中线,又是底边上的高;
等腰三角形底边上的中线,既是底边上的高,又是顶角平分线;
等腰三角形底边上的高,既是底边上的中线,又是顶角平分线这3个角度去思考,也就杜绝了往届学生出现的片面性的问题.
(二)利用好每个几何例题
1.循序渐进:一问,二问,三问
课堂提问需以学生的认知为起点,以学生的需求为导向,以学生的发展为目标.
案例 1:点A是△BCD两个内角∠BCD和∠BDC的角平分线的交点,试探究∠CAD与∠B的关系.
从学生的基础出发先给学生设置梯度小问:
问题(1):若∠B=60°,则∠CAD的度数为多少?
问题(2):若∠B=80°,110°,则∠CAD的度数分别为多少?
问题(3):由(1)(2)你能得出什么结论?当∠B的度数发生变化时,你的结论仍成立吗?
问题(4):根据上面的提问,请尝试通过改变问题的条件,自编一道探究∠CAD与∠B关系的题目.

教学活动不能止步于此,要以学生的发展为目标,教师可以趁着学生学习热情高涨,自然而然地呈现一道变式题,要求学生尝试通过改变现有条件,再自编一题来探究结论.这个看似简单,实则内含深意的做法,充分调动了学生的能动性,也让学生进一步体会条件对于几何题的重要性,当然探究结果也会随着条件的变化而发生改变,此时这节课的高潮也就不期而至.
2.循循善诱:启发,提示,引导
我们的教学要以学生的认知为起点,并不是每一位学生都有自编题的能力,一部分同学会有一种迷茫、无从下手的感觉,这时就需要教师给学生一些启发性的提示,为学生能力的提高搭好阶梯.老师可以提问“原题的条件是什么?那么这个条件我怎么改才能保留我现在想探究的这个角?图形中除了三角形的三个内角还有哪些角?三角形的内角除了平分还可以怎么分?”
此时学生就能提出问题:“老师,如果把它改成一个内角、一个外角的角平分线会怎么样?老师,如果把它改成两个外角的角平分线会怎么样?老师,如果把它改成两内角三等分线的交点会怎么样?把它改成两内角四等分点的交点会怎样?”
教师这些启发性的提示不仅是提高学生解决问题的能力的过程,更是以学生的需求为导向,以学生的发展为目标,努力实现学生的自我知识建构的过程.整个教学过程教师没有一味地“教”,而是让全体学生沉浸在完整真实的学习过程中,充分发挥了学生的能动性,让整个学习过程充实且具有挑战.
所谓的“寻”,主要是“层层推进—由简单到复杂(由特殊到一般)—感悟经验转化为知识”这一过程.经验的提炼有两种状态:一种是自发的,比较零散、模糊、原生态;
另一种是自觉的,是教师通过创造条件让学生总结经验的内省过程.
(一)巧寻:一题多解
证明一个结论正确,可能有多种方法,虽然最后我们都能将结论证得,但中间所花费的时间和精力有着极大的差异.寻找最优基本图形不仅需要对题目给出的条件进行筛选,更需要对基本图形的熟练运用.

图1
案例2(浙教版八上P35课内练习第二题):已知:如图1,AD垂直平分BC,D为垂足.DM⊥AC,DN⊥AB,M,N分别为垂足.求证:DM=DN.
方法一:抓住基本图形“角平分线上的点到角两边的距离相等”(题目中有条件“DM⊥AC,DN⊥AB”,即有从同一点出发到两条边的距离,若AD为∠CAB的角平分线,那就可以运用角平分线的性质来证明,而根据已知条件比较容易证得AD为∠CAB的角平分线).
方法二:抓住基本图形“面积相等的两个等底三角形等高”(题目中有条件“AD垂直平分BC,DM⊥AC,DN⊥AB”,由线段垂直平分线上的点到线段两端的距离相等得到AC=AB,那么只要再证△ACD的面积和△ABD的面积相等即可,根据全等图形的面积相等可证得,而根据已知条件比较容易证得△ACD≌△ABD).
方法三:抓住基本图形“全等三角形的对应边相等”(题目中有条件“DM⊥AC,DN⊥AB”,可得∠AND=∠AMD=90°,又从图中观察得到AD为公共边,只要再寻找一对角相等即可证明△AMD≌△AND,而根据已知条件比较容易证得AD为∠CAB的角平分线).
方法四:抓住基本图形“全等三角形的对应边相等”(题目中有条件“DM⊥AC,DN⊥AB”,可得∠BND=∠CMD=90°,又根据条件“AD垂直平分BC”易得CD=BD,只要再寻找一对角相等即可证明△CMD≌△BND,而根据已知条件比较容易证得△ACD≌△ABD,进而得到∠B=∠C).
上述四种解题方法,方法一和方法二明显优于方法三和方法四.在新课教学时,教师可以展示所有的方法,帮助学生熟练掌握三种基本图形,但最后一定要让学生自主比较到底哪一种“基本图形”对于这个题目的解决更有效.
(二)妙寻:一图多用
几何证明题分为易得分题和易失分题,易失分题又分为两类:一类是图形中重叠交错的线段特别多的,另一类是需要添加辅助线来构造基本图形的.当图形较为复杂时,需要把图形拆分,然后将题目中的条件标到拆分图上,这样就很容易解决问题.
案例3:如图2,面积为1的△ABC.第一步:延长△ABC各边,延长AB至点A1,延长BC至点B1,延长CA至点C1,使A1B=2AB,B1C=2BC,C1A=2CA,顺次连结得△A1B1C1.第二步:延长△A1B1C1各边,使A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连结得△A2B2C2,…,按此方法,要使得到的新三角形的面积超过2022,最少经过________步.

图2
解题思路是将图形做如下三步分解:
第一步:找出原始图形△ABC;
第二步:找出经过一次操作后的图形△A1B1C1;
第三步:将△A1B1C1进行分割并进行相应的计算.连结BC1,∵C1A=2CA,∴S△ABC1=2S△ABC,同理S△A1BC1=2S△ABC1=4S△ABC,∴S△A1AC1=6S△ABC,同理S△A1BB1=S△CB1C1=6S△ABC,∴S△A1B1C1=19S△ABC=19.∴同理可证△A2B2C2的面积=19×△A1B1C1的面积=361,第三次操作后得到的三角形面积为19×361=6859.故按此规律,要使得到的三角形的面积超过2022,最少经过3步.
教师在这个时候能够做的是不断地为学生搭好“脚手架”,鼓励学生自己去发现、提出、分析、解决问题,不断地猜想验证,体会再猜想再验证的思考过程,在不断地失败和成功中提高自己的数学能力.
所谓的“悟”,主要是“破茧成蝶—知识转化为能力”这一过程.杜威认为,教师的教学没有与学生的经验对接,那么教学没有发生.教什么比怎么教更重要,那么到底要教学生什么?学生一节课下来到底要学什么?教师要让学生看到知识的“来龙”与“去脉”.从直观想象到理性思维是一个长期渗透熏陶的过程,直观想象不是无根之萍、乱想象,它是建立在知识基础上的一种感觉,是建立在强大的数学思想与数学思维之上的一种想象.
(一)己悟:认知碰撞
案例4(浙教版八上P35例7):已知:如图3,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.

图3
方法一:抓住基本图形“角平分线上的点到角两边的距离相等”(题目中有条件“PB和PC分别平分∠ABC和∠DCB”,当角平分线的定义无法解决问题时,就要考虑运用角平分线的性质,而要用角平分线的性质就要用到垂线段,没有垂线段就要构造,此题已有条件“AD过点P,且与AB垂直”,那么只需构造BC边上的垂线段即可,如图4.再利用两次角平分线的性质就可以通过等量代换得到DP=AP).

图4
方法二:抓住基本图形“全等三角形的对应边相等”(如图5,延长BP交CD于点F.根据题目中的条件“AB∥CD”与对顶角相等可得△ABP和△DFP的三对内角都相等.而AB与DF无法证得相等,那么只能去证BP=FP,再次运用“全等三角形的对应边相等”这一基本图形,去证明BP=FP,也就是去证明△BCP≌△FCP,证明这两个三角形全等用AAS易证得).

图5
虽然方法一与方法二选择的基本图形不同,但都是通过添加辅助线去构造基本图形,思路也都比较清晰.仔细观察可以看出方法一所耗费的时间与精力明显少于方法二,且证明步骤仅为方法二的一半,故在根据已有条件构造基本图形时也需要选择最优的“基本图形”.
(二)助悟:认知再构建
学生在认知过程中,多次接触选择“角平分线上的点到角两边的距离相等”这一基本图形优于“全等三角形的对应边相等”这一基本图形的几何证明题,那是不是说明所有的题目都应选择构造“角平分线上的点到角两边的距离相等”这一基本图形为最优基本图形呢?其实也不见得.
案例5:上这节新课时,笔者把浙教版八上P35例7进行了改编,去掉了一个条件“AD垂直于AB”,变为“已知:AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P.求证:PA=PD.”
方法一:抓住基本图形“全等三角形的对应边相等”(如图6,延长BP交CD于点F.根据题目中的条件“AB∥CD”与对顶角相等可得△ABP和△DFP的三对内角都相等.而AB与DF无法证得相等,只能去证BP=FP,再次运用“全等三角形的对应边相等”这一基本图形,去证明BP=FP,也就是去证明△BCP≌△FCP,证明这两个三角形全等用AAS易证得).
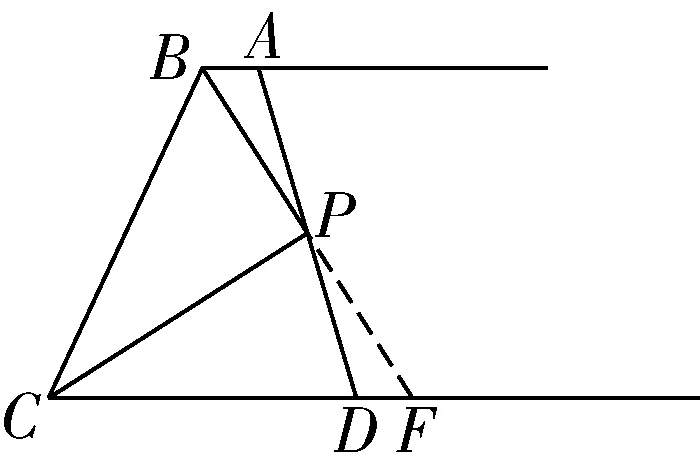
图6
方法二:抓住基本图形“角平分线上的点到角两边的距离相等”(题目中有条件“PB和PC分别平分∠ABC和∠DCB”,当角平分线的定义无法解决问题时,就要考虑运用角平分线的性质,而要用角平分线的性质就要用到垂线段,没有垂线段就要构造,过点P做EF垂直AB,如图7,再利用例7的方式构造BC边上的垂线段,利用两次角平分线的性质就可以通过等量代换得到EP=FP,最后再通过证明△AEP与△DFP全等,利用“全等三角形的对应边相等”这一基本图形得到AP=DP).

图7
很明显,方法一选择的“全等三角形的对应边相等”这一基本图形明显优于方法二选择的“角平分线上的点到角两边的距离相等”这一基本图形,方法二不但添加了两次辅助线,增加了证明难度,最后证得结论时依旧要选择“全等三角形的对应边相等”这一基本图形,证明过程也比方法一长.故并没有选择哪一个基本图形最优的固定模式,而是需要根据题目的条件进行选择,同时辅以直观想象能力的培养.
综上所述,在课堂教学过程中,教师要弱化自己的“教”以及教什么,而是要强化学生的“学”,帮助学生构建知识体系,并且使用不同的教学形式来激励学生更主动的学习,激发他们的学习欲望.解题“悟性”是一种高阶思维能力,绝不是靠一节课、一道题就可以培养起来的,它需要潜移默化的熏陶(“品”),又要持之以恒地训练(“寻”).在这个“寻”的过程中,作为教师要给学生提供感兴趣的切入点以及体验过程,做到以人为本,潜心研究教学,从而科学地引导学生,进而能够启发学生进行合理的知识建构.
猜你喜欢 平分线证明三角形 玩转角的平分线中学生数理化·七年级数学人教版(2021年9期)2021-11-20获奖证明南方医科大学学报(2021年10期)2021-11-10判断或证明等差数列、等比数列新世纪智能(数学备考)(2021年11期)2021-03-08角平分线形成的角中学生数理化·七年级数学人教版(2020年9期)2020-11-16多用角的平分线证题中学生数理化·七年级数学人教版(2019年9期)2019-11-16三角形,不扭腰文理导航·科普童话(2017年7期)2018-02-10三角形表演秀小天使·四年级语数英综合(2017年6期)2017-06-07如果没有三角形小天使·二年级语数英综合(2017年3期)2017-04-01折叠莫忘角平分线中学生数理化·七年级数学人教版(2017年2期)2017-03-25画一画小学生导刊(低年级)(2016年6期)2016-07-02